前面分析了同步發電機對不同性負載供電時的電樞反應的情況，下面通過等效電路和向量圖進一步分析發電機負載運行時各量之間的相互關系和變化規律。

 

 

當隱極式發電機接有三相對稱負載時，電樞繞組中將有三相對稱電流流通，這時在氣隙中除轉子主磁場外，還有電樞磁場。這兩個磁場是獨立存在的，即每個磁勢各自產生自己的磁通，并且在定子繞組產生對應的電勢，發電機總的電勢等于這些電勢的合成。這樣，便得到下列磁通和對應的電勢。

 

ⅰ。主磁通φ和電勢E0。

 

ⅱ。電樞反應磁通φs和電勢Es。

 

ⅲ。定子漏磁通φL和漏磁電勢EL。

 

這些電勢均滯后對應的磁通90°，并和磁通大小成正比。

 

因為Es是Fs產生的電勢反應電勢，當磁路處于不飽和狀態時，Fs和φs是線性關系，則電樞反應電勢Es可用Is在電抗Xs上的壓降來表示，其有效值為

 

Es=IsXs                       （2-31）

 

用符號法表示為

 

Es=-jIsXs                     （2-32）

 

即Es滯后于Is90°。式中，Xs稱為電樞反應電抗。電抗是說明磁場狀況的電路參數。同步發電機Xs越大，說明在一定的電樞電流下，電樞磁勢所產生的電樞磁場就越強，由此磁場所產生的電勢Es也就越大，因此，Xs的大小反映電勢反應的強弱。

 

對于漏磁通，由于它的路徑主要是空氣，故漏感應電勢EL和電樞電流Is也是線性關系，其向量關系為

 

EL=-jIsXL                     （2-33）

 

則EL滯后于Is90°。式中，XL為定子一相繞組的漏電抗。

 

同理，當負載運行時，Is在定子繞組上也將產生電壓降，即

 

U=IsR                         （2-34）

 

由于電樞三相繞組是對稱的，因此，只需分析其中一相即可。

 

根據基爾霍夫第二定律，可列出電樞回路（如A相）的電勢方程式為

 

E0+Es+EL=U+IsR                 （2-35）

 

或

 

E0=U+IsR-Es-EL

 

=U+IsR+jIs（Xs+XL）

 

=U+IsR+jIsXt                 （2-36）

 

式中  Xt——稱為隱極式發電機的同步電抗，Xt=Xs+XL。

 

從電路角度來看，上式說明，發電機每相繞組相當于有一個電勢E0和一定大小的內阻抗的電源，可用圖2.110等效電路來表示。如果忽略定子繞組上的電阻壓降，則發電機一相繞組中的電壓平衡方程式為

 

E0=U+jIsXt                    （2-37）

 

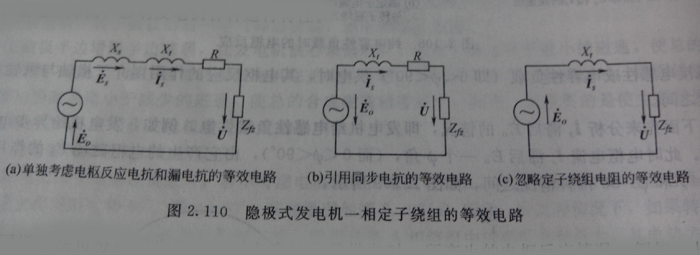
其等效電路和直流發電機的等效電路相似，只不過用同步電抗Xt代替直流發電機的電樞電阻rs而已，如圖2.110（c）所示。

 

同步電抗Xt反映了電樞反應磁場和定子漏磁場共同對定子繞組的作用。在磁路不飽和的條件下，這兩個磁場對定子繞組端電壓的影響，可以用電抗壓降的形式來表示。

 

同步發電機定子一相繞組中的電壓平衡關系可用向量圖來表示。加熱發電機供電于電感性負載，根據負載功率因素角φ，做出定子每相繞組端電壓U和定子每相電流Is的向量，然后在電壓向量的末端加上同步電抗壓降jIsXt，它的相位超前電流Is90°，相連向量U的始端和jIsXt的末端，便得電勢E0的向量，如圖2.111（a）所示。

 

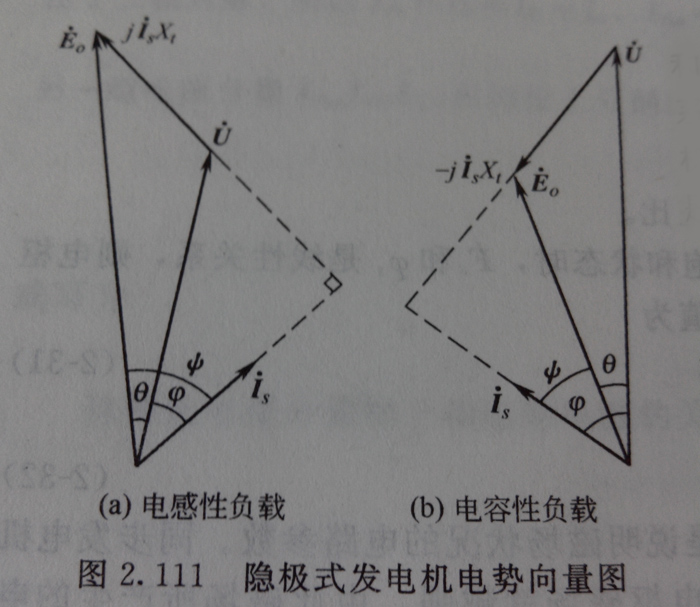
對電容性負載，因Is的相位超前于U一個φ角，用同樣方法可得電容性負載的向量圖，如圖2.111（b）所示。由圖可見它的空載電勢E0比端電壓U小，說明電容性負載電樞反應的助磁作用。

 

應當指出，上面介紹的向量圖雖然沒有考慮磁路飽和，但是它清楚地表面了電勢、電壓和電流之間的關系，這是分析發電機運行特性的基礎。然而，實際發電機的磁路總是飽和的，因此，利用向量圖去分析具體問題時，應加以必要的修正，使得結果更符合實際情況。